Lời giải câu 27, 38, 49 đề thi thử THPT Quốc gia môn toán- Đề tham khảo số 2
Câu 27: Tính tích phân $I=\int_{0}^{2017 \pi}(\sin x+\cos x)e^{x}dx$.
A. I=3.
B. I=1.
C. I=0.
D. I=2.
Giải: Đáp án C.
$\int_{0}^{2017 \pi} (\sin x+\cos x)e^{x}dx=\int_{0}^{2017 \pi} \sin x . e^{x}dx+\int_{0}^{2017 \pi}\cos x. e^{x}dx=A+B$
Tính $A=\int_{0}^{2017 \pi} \sin . e^{x}dx=\int_{0}^{2017 \pi}\sin xd(e^{x})=\left.\begin{matrix}(\sin x. e^{x})\end{matrix}\right|_{0}^{2017 \pi}-B=-B$.
Vậy $I=B-B=0$.
Câu 38: Cho khối chóp S. ABCD có thể tích V và đáy là hình bình hành. gọi M là trung điểm của cạnh SA, N là điểm nằm trên cạnh SB sao cho SN=2 NB, mặt phẳng $(\alpha)$ di động đi qua các điểm M, N và cắt các cạnh SC, CD lần lượt tại hai điểm phân biệt K, Q. Tính giá trị lớn nhất của thể tích khối chóp S.MNKQ.
A. $\frac{V}{2}$.
B. $\frac{V}{3}$.
C. $\frac{3V}{4}$.
D. $\frac{2V}{3}$.
Giải: Đáp án B.
Gọi $a=\frac{SK}{SC}, (0\leq a \leq 1)$
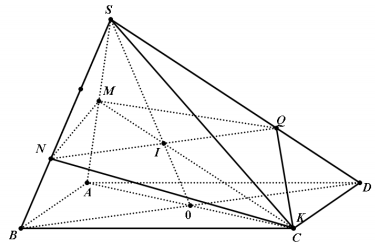
Vì mặt phẳng $(\alpha)$ di động đi qua các điểm M, N và cắt các cạnh SC, SD lần lượt tại hai điểm phân biệt K, Q nên ta có:
$\frac{SA}{SM}+\frac{SC}{SK}=\frac{SB}{SN}+\frac{SD}{SQ}\Leftrightarrow 2+\frac{1}{a}=\frac{3}{2}+\frac{SD}{SQ}$ $\Leftrightarrow \frac{SD}{SQ}=\frac{a+2}{2a}\Leftrightarrow \frac{SQ}{SD}=\frac{2a}{a+2}$.
$\frac{V_{S.MNKQ}}{S.ABCD}=\frac{1}{2}(\frac{SM}{SA}.\frac{SN}{SB}.\frac{SK}{SC}+\frac{SM}{SA}.\frac{SK}{SC}.\frac{SQ}{SC})=\frac{1}{2}[\frac{1}{3}a+\frac{1}{2}a.\frac{2a}{a+2}]=\frac{1}{2}(\frac{4a}{3}-\frac{2}{a+2})$.
Xét hàm $f(x)=\frac{4x}{3}-\frac{2}{x+2}, (0 \leq x \leq 1)$. Ta có
$$f'(x)=\frac{4}{3}+\frac{2}{(x+2)^{2}}>0 \forall x \in [0,1]$$
Suy ra giá trị lớn nhất của hàm f(x) là $f(1)=\frac{2}{3}.$
Vậy giá trị lớn nhất của thể tích khối chóp $S.MNKQ$ là $V_{SMNKQ}=\frac{1}{2}.\frac{2}{3} V_{SABCD}=\frac{1}{3}V$.
Câu 49: Cho ba điểm A, B, C lần lượt nằm trên ba trục tọa độ Ox, Oy, Oz ( các điểm này không trùng với gốc tọa độ) thỏa mãn $AB^{2}+BC^{2}+CA^{2}=8$. Gọi I là tâm mặt cầu ngoại tiếp tứ diện OABC. Biết rằng khi A, B, C di chuyển thì điểm I nằm trên một mặt cầu cố định. Tính bán kính R của mặt cầu đó?
A. R=1.
B. R=2.
C. $R=\sqrt{2}$.
D. $R=\frac{\sqrt{3}}{2}$.
Giải: Đáp án A.
Gọi A(a,0,0), B(0,b,0), C(0,0,c) $(a, b, c \neq 0)$.
Ta có $AB=\sqrt{a^{2}+b^{2}}, BC=\sqrt{b^{2}+c^{2}}, CA=\sqrt{c^{2}+a^{2}}$.
Từ $AB^{2}+BC^{2}+CA^{2}=8 \Rightarrow a^{2}+b^{2}+c^{2}=4$.
Tính $OI=(\frac{c}{2})^{2}+(\frac{\sqrt{a^{2}+b^{2}}}{2})^{2}=\frac{a^{2}+b^{2}+c^{2}}{4}=1$.
Vậy I luôn nằm trên mặt cầu tâm O có bán kính bằng 1.
Bình luận